Scattering techniques are ideal for investigating the structure and interactions in soft matter. However, it is non-trivial to relate the measurements to structural properties of the scattering objects and their interaction. It is therefore of crucial importance to obtain expressions for the scattering intensity (cross section) which can be used for interpreting experimental data, for example, obtained by SAXS, SANS and light scattering. Monte Carlo simulations are ideally suited for developing the models for systems with many degrees of freedom, as the structure can be simulated in real space and the corresponding scattering cross section can be calculated. As the structure and interactions are known in real space, the models can be developed by fitting to the simulated scattering data and by comparing the derived results to the know structure.
Example 1: Block copolymer micelles: (Carsten Svaneborg’s PhD thesis, 2001)
A di-block copolymer consists of two chemically distinct linear polymer chains covalently linked together. When dissolved in a solvent, which is only a good solvent for one block, micelles form. The micelles can have a spherical core as shown in the picture below. The cores are surrounded by a corona of solvated chains. The micelles can be modelled as a dense core surrounded by a diffuse corona of chains interacting through hard sphere excluded volume interactions. Chains are furthermore excluded from the core region.
At a zero-level approximation one can neglect the fact that the corona consists of chains, and assume it is a just radial density profile decaying away from the micellar core. This level of approximation provides core-shell models, and one can get an estimate of the width of the profile using such a model. All chain information has been averaged out, and therefore no information is available on single chain properties. However, the simulation results show that adding an effective single chain scattering expression in the form of a RPA approximation to the core-shell model provides an expression in agreement with the simulated scattering data. This is in effect the scattering one would get from a semi-dilute solution with a radial concentration profile.
The new model provides a very accurate representation of the micellar scattering within the statistical errors for reduced surface coverages less than one, and a very good fits are obtained for all the simulated surface coverages, e.g. reduced surface coverages less than 5. The reduced surface overage is the analogy to c/c* of polymer solutions. This result is obtained and validated for micelles (with a spherical core). However, the instantaneous density distribution of any tethered chain structure can be regarded as an average density distribution, and an instantaneous density fluctuation distribution. Thus the scattering can be regarded as arising from the Fourier transform of these two distributions. A fluctuation-dissipation theorem relates the zero-mode Fourier component of the density fluctuation distribution to the osmotic compressibility of the system.
The new model when applied to experimental scattering data provides the radius of gyration, corona osmotic compressibility/corona apparent second osmotic virial coefficient, as well as information on the shape of the radial profile. The model should furthermore be easily generalizabled to any tethered chain structure, where chains are not stretched too much, and concentration is locally in the dilute semi-dilute regime such that an RPA approximation is valid.
For the figure below, a standard micelle was chosen as having 44 chains, 50 bonds per chain, and a core radius of 10/3 b, where b is the Kuhn length. A chain has 8.33 statistically independent segments, and the micelle a reduced surface coverage of about 4 (the analogy to c/c* of polymer solutions). The experimental range of diblock copolymers is a reduced surface coverage less than five. The spheres in the picture illustrates the range of the hardcore excluded volume interactions. The radius (e) of the excluded volume hard spheres was chosen as (e/b=0.1) in order to mimic polystyrene in a good solvent.

Example 2: Monte Carlo Simulations of Polymers and Polyelectrolytes (PhD thesis of L. Cannavacciuolo, ETH-Zürich, Switzerland, 2001)
The effect of electrostatic interactions on the flexibility of polyelectrolytes has been the subject of intense experimental and theoretical investigations and resulted in highly controversial results. The persistence length of polymers and polyelectrolytes is often determined by scattering methods such as small-angle neutron (SANS) or x-ray (SAXS) scattering. The problem with conventional polymer polyelectrolytes is their rather weak scattering power when performing SANS or SAXS experiments, which makes it almost impossible to produce data with a sufficient quality over the required range of scattering vectors q at low concentrations, where single-coil properties still can be resolved. We have studied experimentally and by Monte Carlos simulations solutions of polymer-like micelles ‘doped’ with ionic surfactants, which can serve as a model system for polyelectrolytes and help to clarify some of the open questions in the literature. However, a major problem in this context is the missing theoretical background for a quantitative interpretation of scattering data from polyelectrolyte solutions.
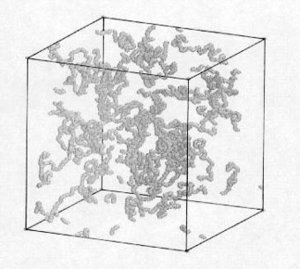
We have performed an extensive Monte Carlo simulation in order to determine the full scattering function of semi-flexible polyelectrolytes as a function of contour length, charge density and ionic strength as well as concentration c of chains. In these simulations we use an extension of a discrete representation of a Kratky-Porod worm-like chain model in the pseudo-continuous limit, which we have modified in order to take into account excluded volume interactions as well as electrostatic interactions (through a screened Coulomb potential) between the chains. We have performed both strictly single chain (c=0) as well as many chain simulations (c finite).
The Figure snapshot of a many chain simulation of wormlike chains with excluded volume interactions.